
研究内容
CAREER
混相流シミュレーション
混相流は気体と液体、固体と液体の界面をクリアに確認でき、流体のダイナミクスを身近に感じることができます。一方、密度が3桁も異なる相が接する気液界面が激しく変形したり、固体境界が移動したりするため、混相流シミュレーションは難易度の高い計算となっています。原子力分野などでは、2000年より前は気液界面を直接扱わず、気体の体積率(ボイド率)で気泡流を計算していました。
2000年以降、気液界面を直接計算する手法が発展してきました。質量保存性に優れるVOF(Volume Of Fluid)法、界面の過剰な拡散を防ぐことができるPhase filed法、高精度な幾何学計算に優れるレベルセット法、Front Tracking法などがありますが、どの方法も気液界面を有限なメッシュ幅(数メッシュ以下)で記述する方法で、カットセルのようなセルの内部で密度の不連続面を記述する方法は余りうまくいっていません。
以下で説明するように、非圧縮性流体の気液二相流に対し、界面捕獲手法にPLIC-VOF 法、表面張力計算にHeight Function(HF)法、Navier-Stokes方程式を運動量保存型の弱圧縮性流体計算手法で解いた結果を示します。ダムブレーク問題を1536×256×768の等間隔格子で計算した結果です。
 |
1536×256×768の等間隔格子で計算したダムブレーク問題
下の左図は気泡径の統計分布を示しており、解析的に予想される半径の-3/2乗のべき乗スケールとよく一致しています。この格子解像度では表面張力が支配的になるHinzeスケールより小さい気泡径までは計算できないことが分かります。右図は液滴径の統計分布であり、解析的に予想される半径の-9/2乗のべき乗スケールとよく一致することが分かりました。
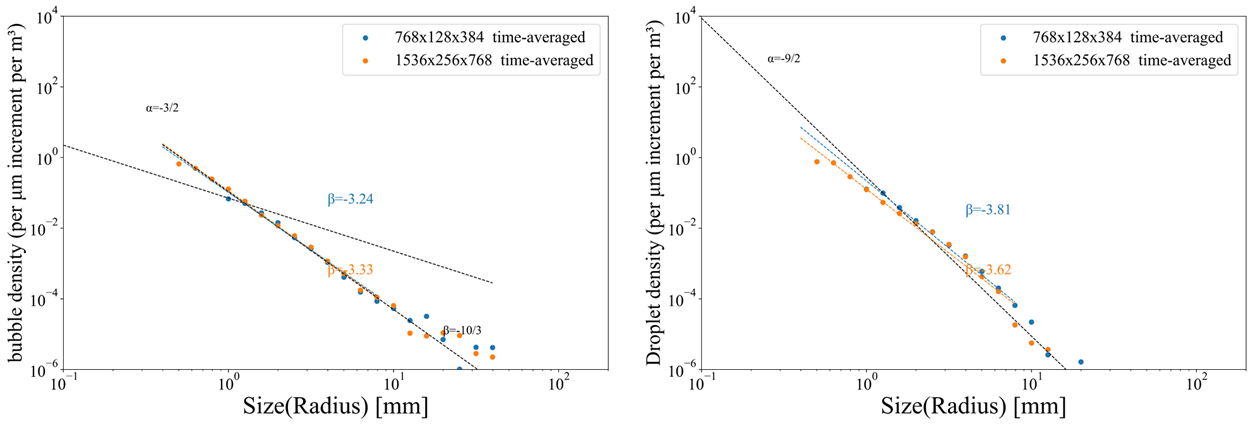
気泡径分布(左図)と液滴径分布(右図)
PLIC-VOF 法
界面捕獲手法として最も広く使われているのがVOF法です。セル内のある相が占める体積割合をVOF値として定義し、VOF値の保存方程式(非圧縮性流体を仮定しているので移流方程式と同じ)を解くことで界面を記述する手法です。有限体積法で解くことで相の体積保存性を保証できる利点があります。我々はVOF法の中で最も界面記述の精度が高く、シャープな界面幅を持つPLIC-VOF 法を用いています。PLIC-VOF 法は幾何的に再構築する手法であり、VOF値からMYC(Mixed Youngs-Centered)法を用いて法線ベクトルを算出し、図のように界面の再構築を行います。図の(a)のαは平面の方程式の切片で、逆問題として計算することができます。これを元にVOF値と運動量の移流計算を行います。3方向同時に移流計算を行うと重複する部分が生じるため、1方向ずつ移流計算を行います。2次元計算の場合、図の(b)のように赤線に囲まれた領域がVOF流束に対応し、時間積分を行います。
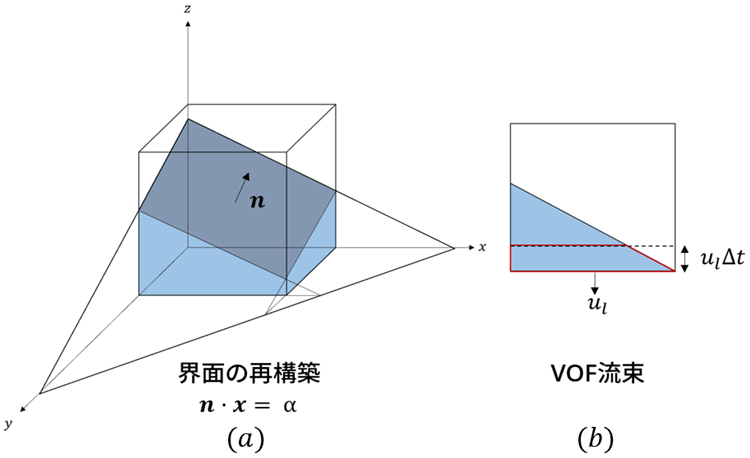
PLIC-VOF法の界面再構築
Height Function(HF)法による表面張力計算
表面張力は気液界面に作用する面積力であり、VOF法やレベルセット法は界面を陰的に表す関数の時間発展を解く手法であるため、界面のみに面積力を作用させることは難しいと言えます。そこで、表面張力の計算には Brackbillらにより提案されたCSF(Continuum Surface Force)モデルを用います。さらにDensity-weighted CSFモデルは計算精度を向上させるために有効です。CSF法は面積力である表面張力を体積力として界面近傍に振り分ける手法であり、陽的に界面を見つける必要がなく、VOF法に対して適切に表面張力を組みこむことができます。レベルセット法を用いた曲率計算は計算セルの中心で曲率を求めるのに対し、HF法は計算セルごとに座標系を定義し、図のように界面を高さ関数として記述して曲率を求めるため、精度の高い曲率計算ができます。
気液二相流のスケールが小さくなると、表面張力が支配的になってきます。流体力学的には圧力と釣り合って静止するような条件でも、数値的に釣り合わないためにしばしば非物理的な疑似流速(Spurious current)が発生してしまいます。左図はレベルセット関数に基づいて曲率を計算した場合に発生する疑似流速を示しています。右図はPLIC法とHF法を組み合わせることで疑似流速を劇的に(1/100以下に)低減することができます。
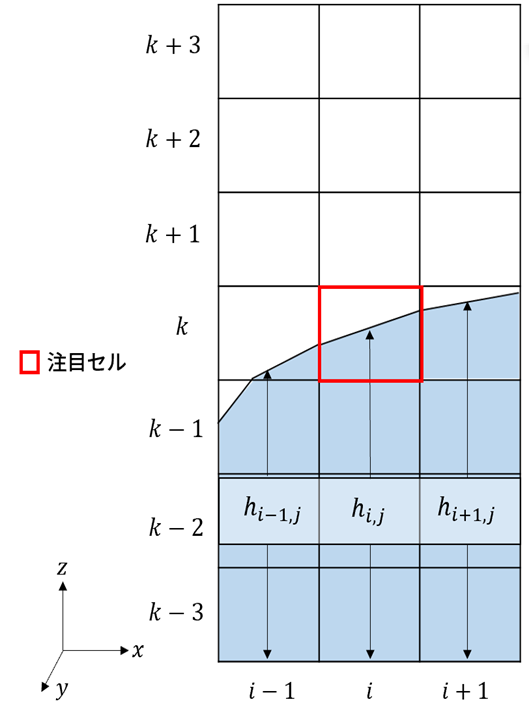
Height Function 法
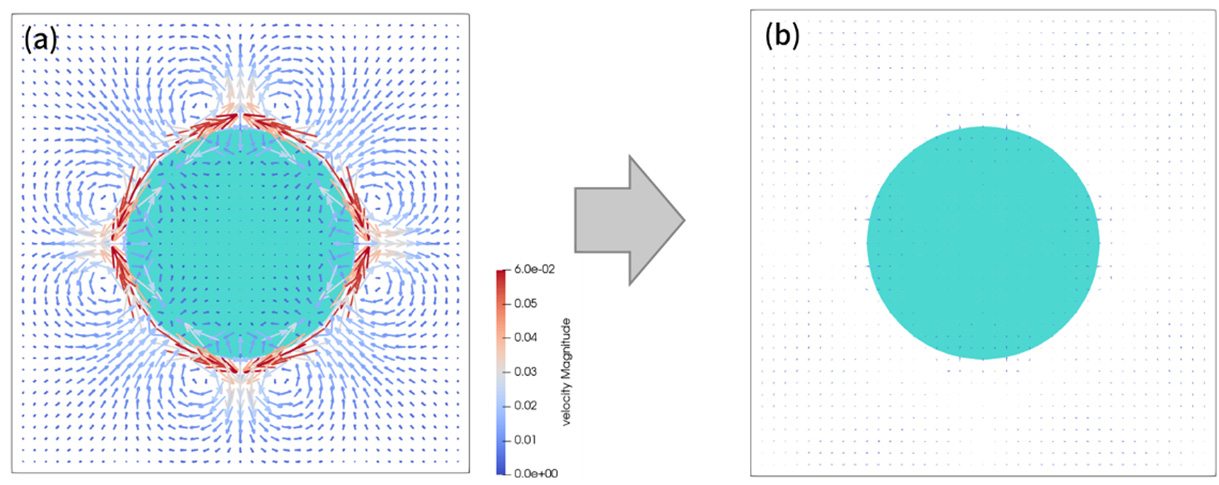
Spurious currentの比較:(a) レベルセット関数による曲率とThinc WLIC法による計算、
(b) HF法による曲率と PLIC法による計算
Navier-Stokes方程式の弱圧縮性流体計算手法
非圧縮性の気液二相流を計算するための圧力のポアソン方程式は非ゼロ要素に流体の密度が入り、複雑な形状の流路や大規模問題などでは解き難い(反復法で収束し難い)連立一次方程式になります。流体はマッハ数(音速に対する流速の比)が0.05程度以下であるとほぼ非圧縮性が成り立つと言われていて、圧縮性のNavier-Stokes方程式に等温過程と低マッハ数近似を適用すると、dp/dt =-ρcs2 ∇・u が得られます。ここで csは流体の音速です。この式は圧力の時間発展方程式であり、Navier-Stokes方程式と合わせて陽解法で解くことができ、弱圧縮性流体計算と呼ばれます。音波伝播を含み、時間発展のΔtは音速で制限されます。
非圧縮性流体として解きたい流れに対して上記の弱圧縮性流体計算手法で解くと、非圧縮性流体の条件∇・u = 0を完全に満足しなくなるため圧縮が生じます。現実の流体にも圧縮性があり、例えば室内の流速 1 m/s 程度の気流を計算する場合に実際の音速340 m/s (マッハ数は0.003)を使うと正しい流れの計算を行うことができます。逆に、非圧縮性流体の条件 ∇・u = 0 は音速を無限大(マッハ数がゼロ)にする近似と言えます。しかし、時間刻みを音速に対してCFL条件を0.5で計算したとしても流速に対するCFL条件は0.5×0.003と非常に小さくなってしまいます。時間刻みが非常に小さくなるために所定の時間まで計算するには膨大な時間ステップが必要になり、計算効率は非常に低くなってしまいます。そこで、実際の音速を使わず、どのような場合もマッハ数が0.05程度になるように人工的に音速を低減します。これにより流体は実際よりも圧縮されますが、非圧縮性流体として十分見なせる∇・u の値になります。状態方程式も必要になるが音波は短時間で減衰するため、気液を問わず理想気体の状態方程式を適用しても問題ありません。
運動量保存型・気液二相流計算手法
Navier-Stokes方程式は運動量保存の方程式であるにもかかわらず、気液二相流に対しては密度を時間・空間微分演算の外に出し、非保存形で速度 に対する時間発展方程式として解いている場合が殆どです。気体と液体の密度は一定ですが、それぞれの領域は時間的にも空間的にも変化しているので、流体の運動量の時間発展として解くべきです。Navier-Stokes方程式を単純に運動量で解くと、速度を求めるには気体から液体まで値が1000倍も変化する密度で運動量を割算しなければならず、これを回避して計算を安定化させているのが非保存形の計算手法です。
気液二相流の場合、重力は密度の大きい液体に大きな力として作用するため気体と液体では流速が異なることが多く、しばしば界面ではせん断流れとなります。例えば海洋の風波は海水の方が重いため海水よりも空気の流れの方が速く、水面で強いせん断速度が発生します。斜面を下る流れなどでは、逆のことが起こります。気液二相流計算では界面に対してVOF法など識別変数を解き、気液界面を2~3格子以上に広がった密度プロファイルとして計算しています。一方、速度プロファイルは非保存形のNavier-Stokes方程式に従って解くと、密度プロファイルとは整合しないプロファイルを持ってしまいます。速い速度の気相側に液相側の高い密度が漏れ出しているため、速度と密度の積である運動量は図のように、その重なった部分で非常に大きな値となります。つまり、非物理的な運動量が液相側に印加され大きな運動量の輸送が起こってしまいます。そこで、運動量と密度の整合性を取ることにより計算を安定化させる運動量保存スキームを用いています。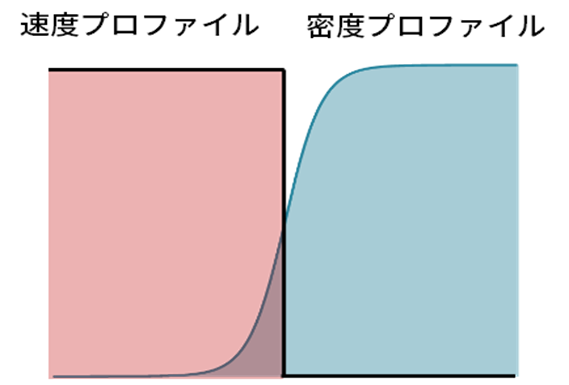
気液界面での速度と密度プロファイルの不整合
ミルククラウンの形成
ミルククラウンの形成は典型的な気液二相流で、上記の計算手法を全て導入したシミュレーションを行いました。これまで多くの実験・シミュレーションが行われてきました。Weber数が250のときのミルククラウン形成の計算条件は、液滴径を7.04 mm、0.82 mmの厚さの液膜に初速度1.61 m/sで衝突させ、OpenFOAMなどのベンチマーク問題の設定と同じとし、最小格子幅は19µmで計算しています。Weber数が250ではフィンガーの数は16本で、格子解像度を上げても結果が変わらなくなる格子収束性が得られています。
 |
| 1536×256×768の等間隔格子で計算したダムブレーク問題 |
Weber数が560のミルククラウンの形成は、実験と比較するために同じ条件の液相と気相の密度、粘度、表面張力係数を用い、初速度4.258m/s 、液滴径 2.1mm、液膜厚さ 0.252mmで計算しています。
実験とシミュレーションが非常によく一致している結果が得られています。最小格子幅を11.8µmから5.9µmに細かくすると、フィンガーの数が27本から32本に増えますが、これ以上細かくしても結果は変わりません。実験結果もフィンガーの数は30本程度となっています。
 |
| 1536×256×768の等間隔格子で計算したダムブレーク問題 |
冠水道路を車が走行する際の水撥ねシミュレーション
時速30kmで進む車が深さ 60mm に冠水した道路を走行する場合の水撥ねを、気液二相流シミュレーションを行いました。激しい気液二相流であるため、運動量保存型のスキームで計算する必要があります。また、気液界面は計算領域の限定された部分のみに存在するため、AMR法も非常に有効です。図の(a)は最小1cmの格子を用い、(b)はタイヤの近傍の3.136m×0.704m×0.32mの範囲を最小格子1mmで計算しています。
 |
 |
| 冠水道路を車が走行する際の水撥ねシミュレーション (a) 最小格子幅1cm、(b) 最小格子幅1mm |
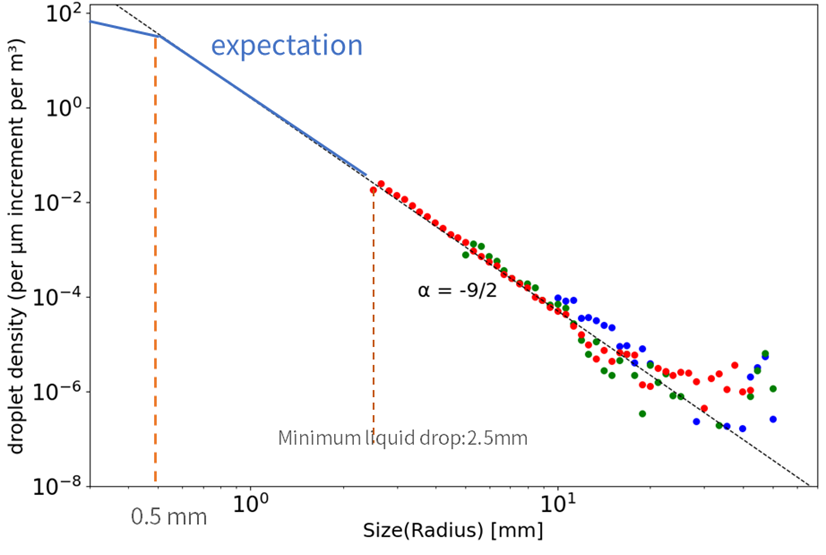
発生した液滴のサイズ分布を調べました。図の青色のドットは最小格子が4mmの計算、緑色のドットは最小格子が2mmの計算、赤色のドットは最小格子が1mmの計算です。理論解析から液滴径分布が半径の-9/2乗のべき乗則に従うと予想されていますが、どの格子サイズで計算した場合もべき乗則によく一致することが分かります。液滴径が0.5mm より小さくなると表面張力が支配的になり、べき乗則の傾きが変わるはずであるが、そこまでの格子解像度には到達していません。ある程度の解像度で計算を行うことにより切片を求めれば、その解像度では表現できない小さな液滴径分布を予測することができます。
気液界面での速度と密度プロファイルの不整合
