研究内容
CAREER

空飛ぶクルマ・eVTOL のフリーフライト・シミュレーション

「空飛ぶクルマ」の将来イメージ

次世代のモビリティとして期待されている「空飛ぶクルマ」と称されるマルチコプターは、2025年の大阪万博で定期運航が見送られるなど、安全性が疑問視されていることは明らかです。大型のドローンのような航空機ですが、無人の場合とは全く異なり、けた違いの航行安全性が求められます。複数の「空飛ぶクルマ」が（特に上下に）接近・衝突してしまったとき、ローターの一つが停止するなどの異常な回転をしたとき、予期せぬ突風にあおられたときなど、どうやって姿勢を立て直し安全な航行を維持するかなどの制御法の確立や、より安全な「空飛ぶクルマ」の設計・開発など、実機による実験は余りにコストと時間が掛かり過ぎます。
そこで、コンピュータの仮想空間の中に「空飛ぶクルマ」を設置し、さまざまな状況下でローター・ブレードに（時間的に変化する）回転数だけを与え、仮想の「空飛ぶクルマ」がどのように航行するのかを予測する（実験に置き換わる）フリーフライト・シミュレーションを実現することを目的としています。

これまでもヘリコプターやドローンのシミュレーションは数多く行われていますが、その全てがローター・ブレードのシミュレーションであり、機体の飛行までをNavier-Stokes方程式を解いてシミュレーションするものは（現時点で調べた限り）存在しません。ブレードが高速で回転するためにレイノルズ数が高く、ブレードにかかる力を計算するには非常に薄い境界層まで解像する高解像度格子をy+に配置する必要があります。このため計算コストが膨大になり、ローターが30回転する程度までの時間しか計算できません。しかし、機体の飛行をシミュレーションするには少なくともローターが1000回転する程度の時間まで計算する必要があります。

計算手法

１．空力計算

高レイノルズ数の乱流に対し、高性能な陰的LES渦粘性により高精度かつ安定な空力解析を行うことができる Cumulant型格子ボルツマン法（LBM）を用いています。境界層の剥離や再付着を精度よく計算できるため、ドラッグ・クライシスも精度よく再現することができます。

「空飛ぶクルマ」同士の（上下）接近や衝突、建物への接近、離陸・着陸などのさまざまな飛行のシミュレーションに対して、移動格子や重合格子は制限が多過ぎるために適用できません。そこで、数100メートル立方の静止した計算空間を用意し、その中で8分木データ構造に基づいたAMR (Adaptive Mesh Refinement) 法により「空飛ぶクルマ」の近傍に高解像度格子を動的に割当て、細分化と粗大化を「空飛ぶクルマ」とともに移動させることにしました。

「空飛ぶクルマ」の形状モデルとAMR格子

「空飛ぶクルマ」の形状データ（STLデータ）からレベルセット関数を作成し、Interpolated Bounce Back法により移動する複雑形状の境界条件をLBMの流体計算に課しています。一方、境界でBounce Back した速度分布関数を用いて「空飛ぶクルマ」にかかる力を求めることができます。

GPUスパコンを用いるため、複数GPUを前提としたコードの実装を進めています。各GPUはシミュレーション内にメモリプールを持ち、AMR格子の細分化と粗大化に伴う頻繁なGPUメモリの確保と解放を避けています。また、空間充填曲線（モートン曲線）を用いた動的負荷分散、GPU間の通信と計算のオーバーラップなども実装しています。

２．アクチュエータライン・モデル

ローターではブレードが高速回転するために流れのレイノルズ数が高く、従来の方法でブレードにかかる力を計算するには、非常に薄い境界層まで解像する格子を用いたLES計算、壁関数法、DES計算のどれかが必要となります。いずれにしてもブレード近傍では非常に高解像度の格子を用いた計算が必要となり、この計算負荷が膨大であるためにブレードが30回転する程度の時間までしか計算できません。そこで、「空飛ぶクルマ」のローター部に、翼素運動量理論に基づいたアクチュエータライン・モデルを用いることにしました。

既にデータベース化されている翼断面に対する揚力・抗力の空力特性を用い、図のようにブレードにマーカー点を設置し、その点に翼素理論に基づいて空気から受ける力をブレードに与えます。一方でその反作用による力をガウシアン・フィルタにより分散して流体に与えます。

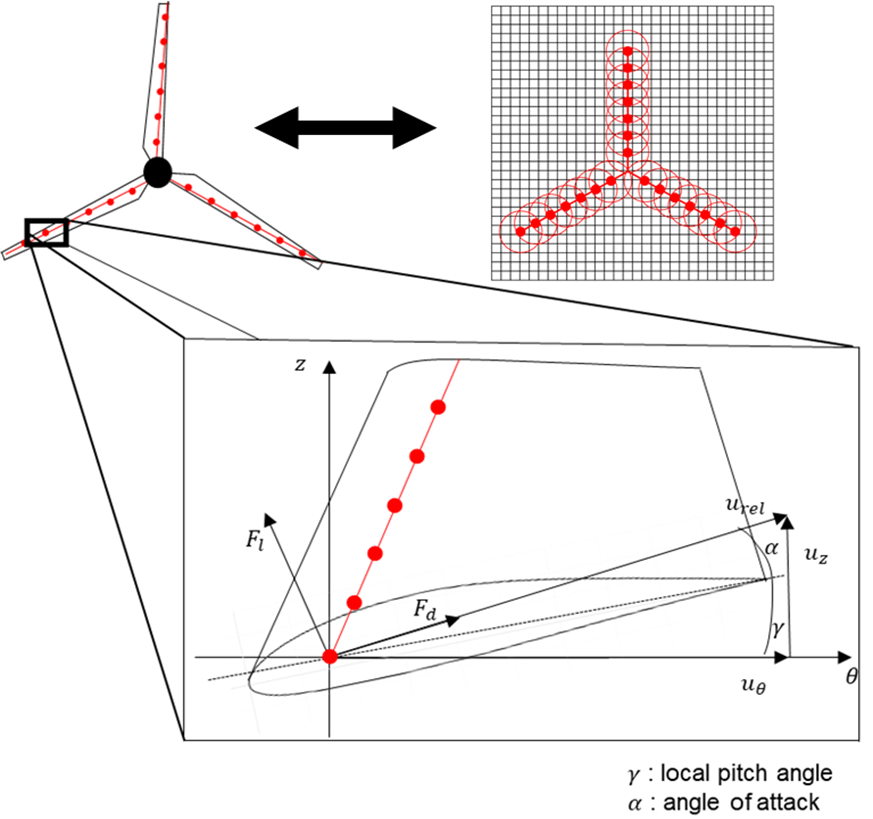
PLIC-VOF法の界面再構築

アクチュエータライン・モデルをローター・ブレードに適用し、実験および詳細なCFD（壁面からの無次元距離 y+ に十分格子を集めた計算）との比較を行い、Single rotor だけでなくCo-axial rotorについても（図のように）実験および詳細なCFDと非常に良い一致が得られました。

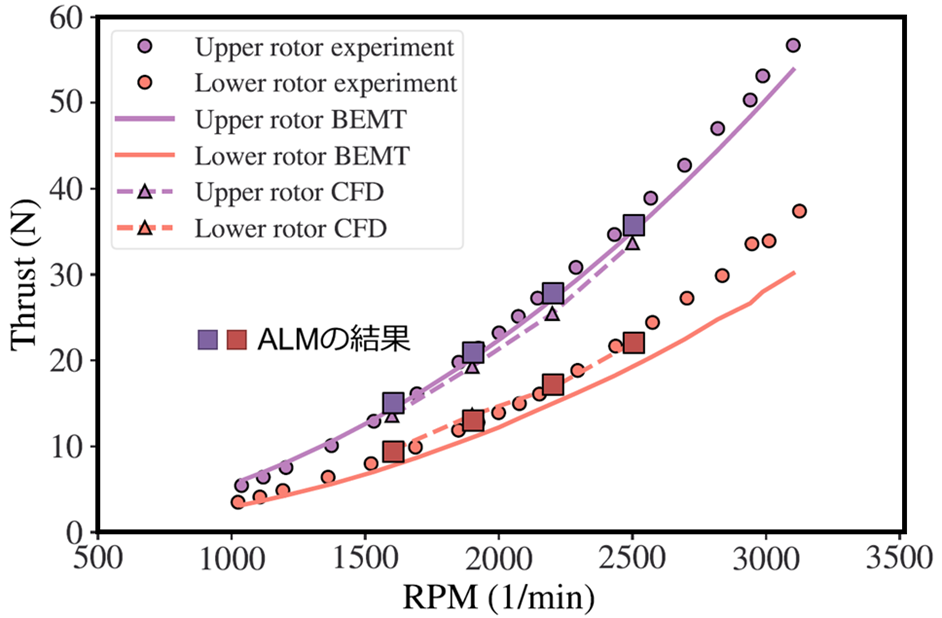
アクチュエータライン・モデルによるCo-axial rotor の推力

PIDフィードバック制御

　「空飛ぶクルマ」のローター部からブレードを削除し、そこにアクチュエータライン・モデルを導入することでローターが受ける推力、周囲の空気から受ける空力を計算できるようになり、重力も加えて機体の運動方程式を解き、機体の運動とそれによる周囲の流れの相互作用を計算しました。
機体に鉛直上下移動のみの自由度を与え、ローターの回転数を指定したときに「空飛ぶクルマ」の自由な上昇・ホバリング・下降ができることを確認しました。また、鉛直方向、水平1軸方向とそれらに垂直な軸周りの自由度を与え、「空飛ぶクルマ」の前後のローターを逆回転させることによる360度のピッチ回転、左右のローターを逆回転させることによる360度のロール回転もできることを確認しました。
ところが、6自由度のシミュレーションを実行すると、動画のようにホバリング中の「空飛ぶクルマ」が姿勢を崩し墜落してしまいます。マルチローターによる飛行は基本的に不安定であり、ドローンの飛行と同じように、PIDフィードバック制御をシミュレータの中に組み込んで計算する必要があることが分かりました。

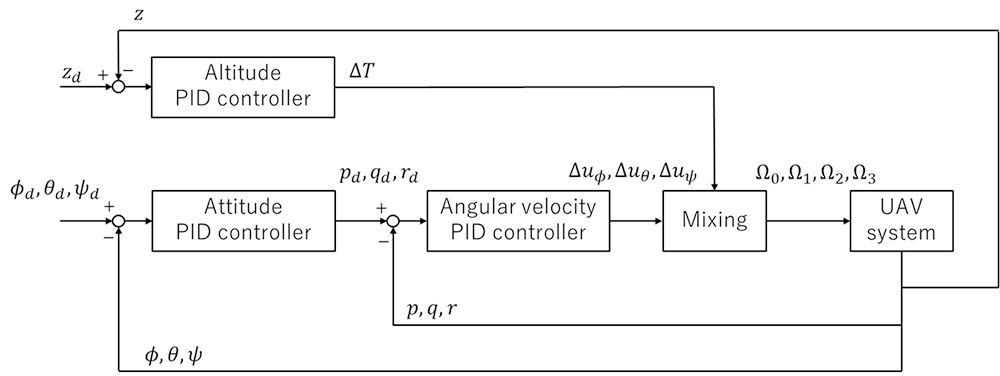
(b) HF法による曲率と PLIC法による計算