研究内容
CAREER

野球ボールの空力シミュレーション

野球は日本や米国などで非常にポピュラーなスポーツです。特にピッチャーの投球は試合の勝敗に大きな影響を与えます。ピッチャーは腕を振り指からボールに力を加え、ボールをリリースします。その際、投げ方を変えることでリリース時のボールの「球速・回転速度・回転軸」を変え、ボール軌道を縦横に変化させたり球速を変えたりして打者に打たれ難いボールを投げます。日本のプロ野球や米国のメジャーリーグ（MLB: Major League Baseball）のピッチャーは球速が130～160km/hで回転数が1,000～2,500 rpmのボールを投げます。ボールには重力以外に周囲の空気が流体力（抗力や揚力）として作用するため、ボールの軌道はさまざまに変化します。

野球のボールには縫い目があり、僅か0.9mmの高さの縫い目の回転がボール周囲の空気の流れに大きな影響を与えます。図のようにボールの進行方向に対して回転軸がほぼ垂直で、打者から見てボールが1回転する中で縫い目が4本見えるフォーシームと2本しか見えないツーシームの2種類の回転が主に使われています。フォーシームはストレート（直球）とカーブに使われます。ツーシームは高速回転でシュートとスライダーに、低速回転ではフォークボール（スプリット）やチェンジアップ、落ちるスライダーなどに使われることが多いようです。ピッチャーによってかなり違います。

野球ボールの空力解析の計算方法

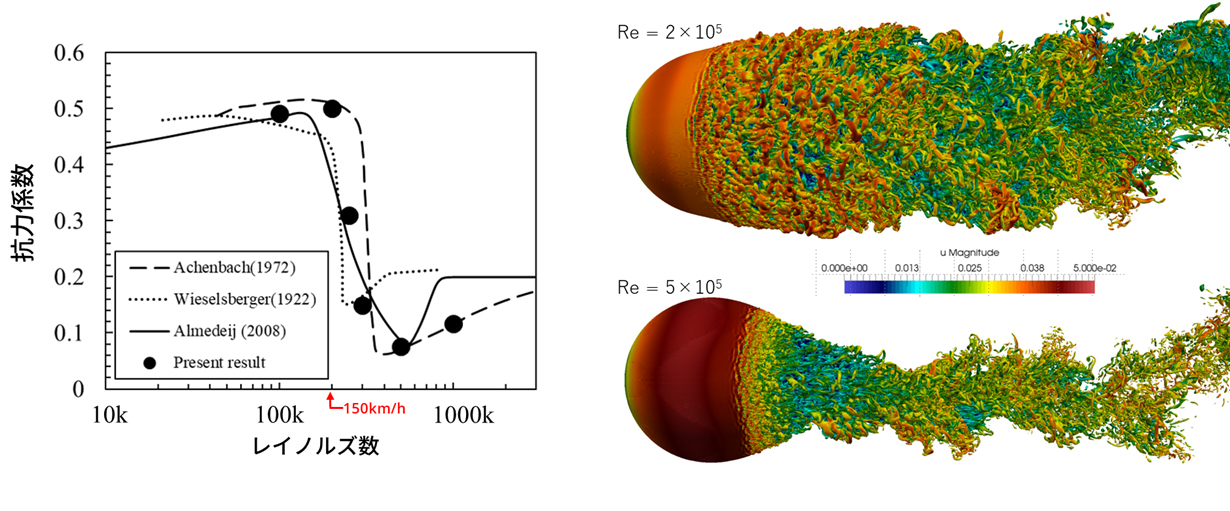
位相空間で仮想粒子（速度分布関数）の並進と衝突に基づいて流体計算を行う格子ボルツマン法（LBM: Lattice Boltzmann Method）を用いています。Chapman-Enskog 展開を用いると、LBMはNavier-Stokes方程式に帰着することが数学的に証明されています。Cumulant 衝突モデルを用いると、陰的なLES (Large-Eddy Simulation) が適切に作用するようになります。Cumulant 衝突モデルのLBMは空力解析には十分な実績があり、一様流中に置かれた球に働く抗力がレイノルズ数Re=200,000～500,000で急激に低下するドラッグ・クライシスを下図のように精度よく再現することができます。

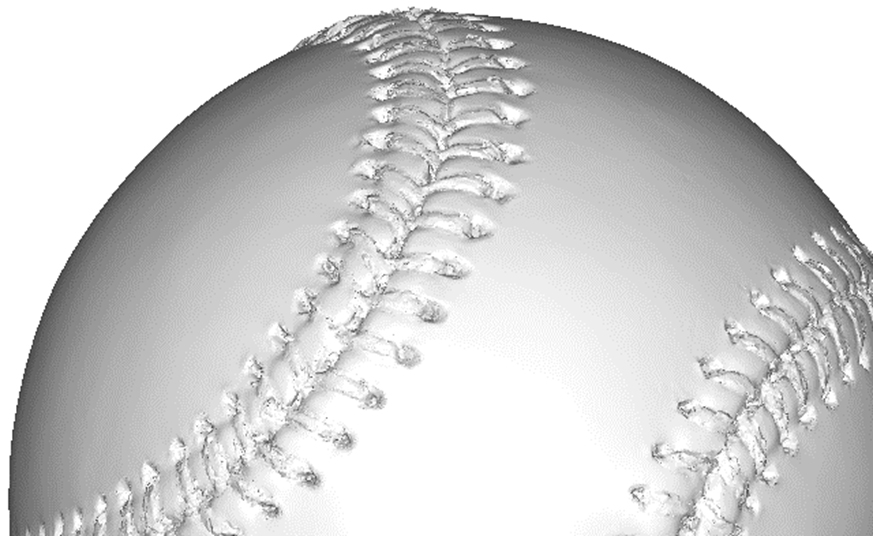
縫い目のある野球ボールの形状を計算に取り込むために、MLB公式球を Keyence VL-500 を使って10μmの解像度で3Dスキャンしました。表面形状をSTLデータとして空力シミュレーション・コードに渡します。

高速で回転しながら飛翔する野球ボールの空力解析を行うには、高解像度格子を用いて計算する必要があります。しかし、計算領域全域を高解像度格子で計算すると莫大なメモリと計算コストがかかります。そこで、AMR (Adaptive Mesh Refinement) 法を用い、高解像度格子で計算する必要のあるボールの表面近傍および後流領域に高解像度格子を集め、効率的に計算しています。

フォークボールが鋭く落ちる理由

野球のピッチャーが投げるフォークボールやスプリット（以下，フォークボール）と呼ばれる球種は、縦に鋭く変化する決め球として、打者に打たれ難いことで知られています。フォークボールは投手が人差し指と中指でボールを挟んで投げ、約1,000～1,500 rpm程度の低速ツーシーム回転です。動画は同じ流速151.2 km/h (Re = 200,000)，回転数1,110 rpmで共通とし、ツーシームとフォーシームという縫い目の違いだけで、ボールの受ける揚力の時間変化が全く異なることが分かります。

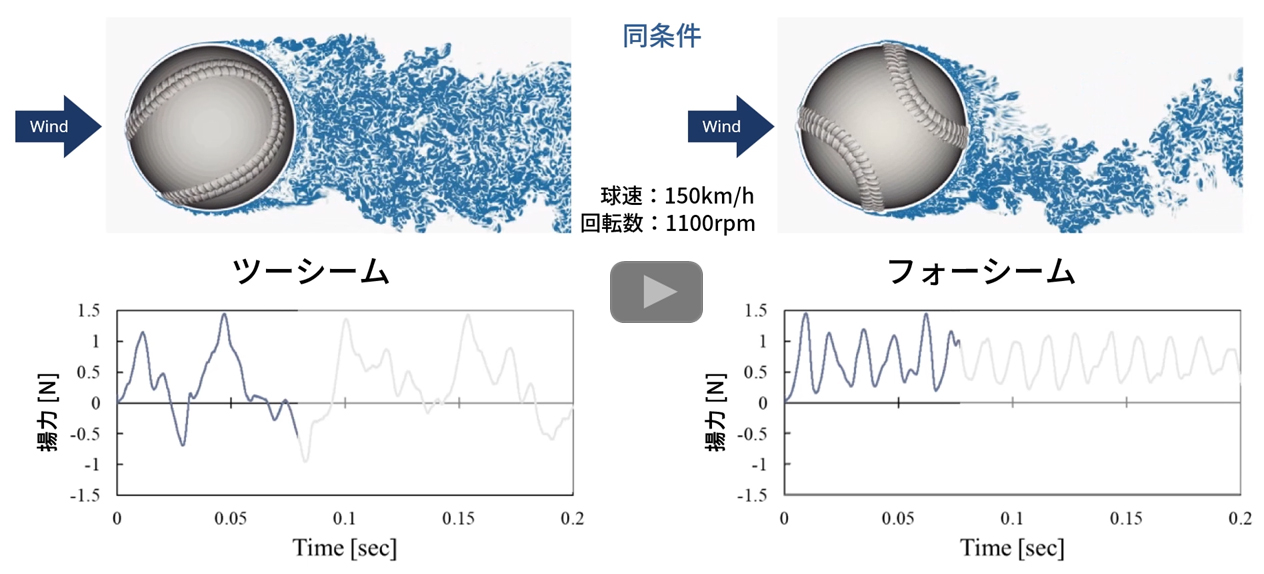進行方向に対してバックスピンの回転になっているため、通常であればボールは回転により浮き上がる正の力（揚力）を受けます。ところが、ツーシームではときどき揚力が負になっています。そこで、各時刻でのツーシームのボール表面の圧力分布および進行方向分布の変化を調べました。右側の上段がボール上面、中段がボール側面、下段がボール下面の分布です。ボールの上面はΦ＝-150°付近から-30°付近までの回転角度の広い範囲で縫い目の影響が殆ど無く、滑面のほぼ真上で層流剥離が起きているます。-30°付近から流れに沿った方向の両脇の縫い目で生じている剥離が中央の滑面での層流剥離に影響し始めます。15°付近では横向きの縫い目により上流からきた流れはほぼ乱流状態となり、そのため境界層の剥離点はかなり上流に移動します。その後は横向きの縫い目が上面を横切り、90°以降では剥離は縫い目に固定され下流に移動するようになります。後流の上下方向の向きに応じた逆方向の反作用がボールにかかります。後流の向きが上向きになる負のマグヌス効果が、縫い目の角度が-150°付近から90°付近まで発生していることが分かります。

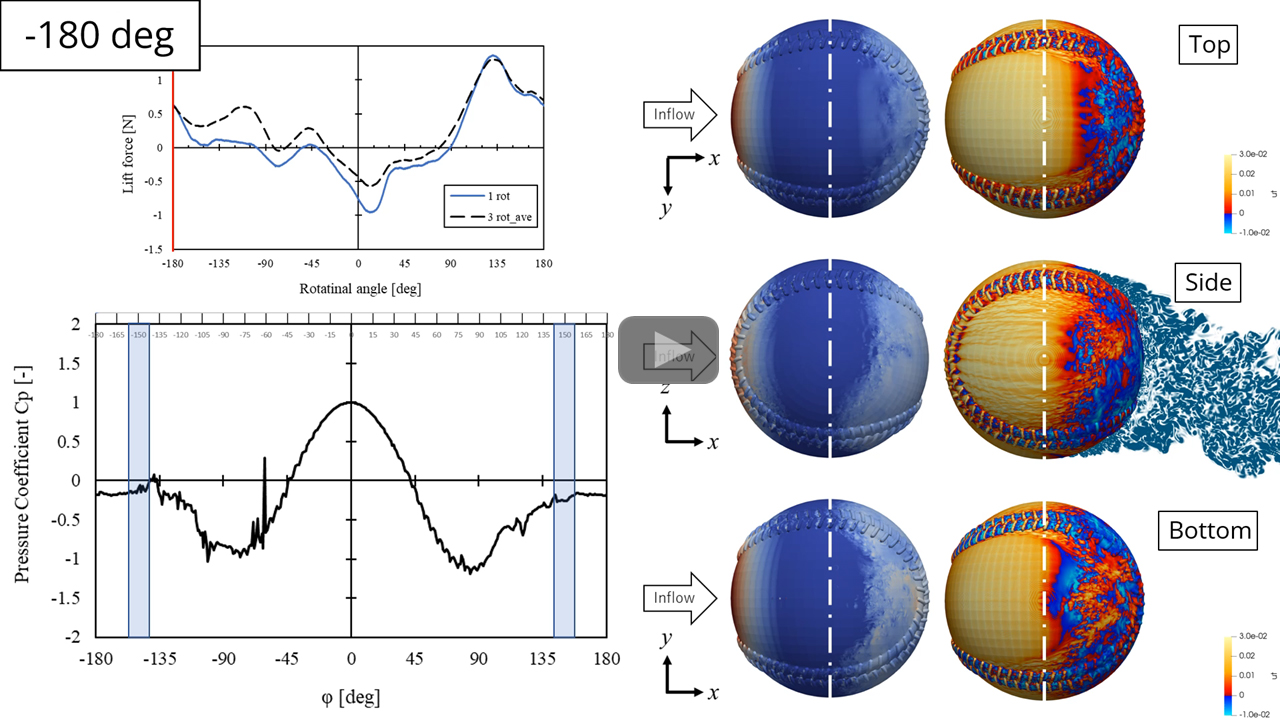一方、フォーシームでは4本の縫い目が境界層の剥離を後方に引きずって（固定して）回転します。回転する突起は正のマグヌス効果を持っているため、縫い目が上下面を頻繁に横切るフォーシームでは負のマグヌス効果が発生しないことが分かります。
これまで実験では硬式野球ボールのフォークボールに対して、『負のマグヌス効果』の発生は確認されていませんでしたが、本数値シミュレーションにより発生していることを初めて見出しました。

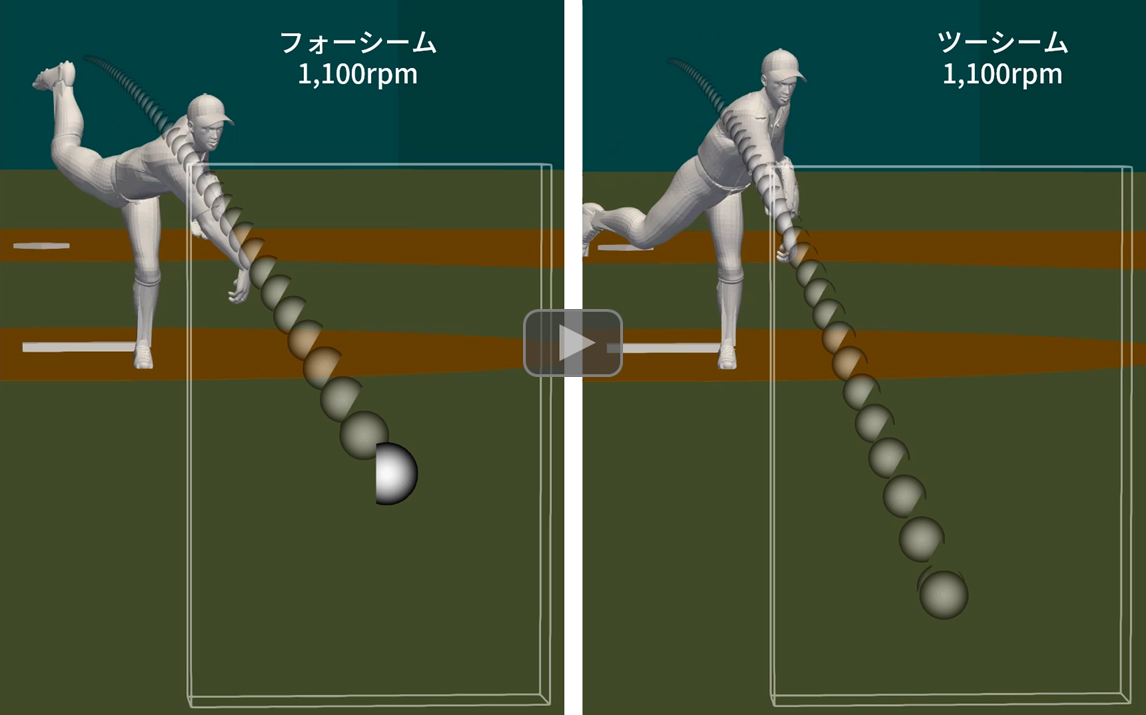これまで、フォークボールは低速回転であるために揚力が小さく、そのために落ちると思われていきました。この研究により、ツーシームは縫い目の角度が-30°から90°の範囲で負のマグヌス効果が発生しているため、バックスピンの回転が少ないことに加え揚力がさらに低下し、ボールの軌道は同じ回転数のフォーシームと比較して打者の地点で19 cmも落差があることが分かりました。

ジャイロスプリット・ボールの変化

MLBで活躍する大谷翔平選手は、2021年は投手としてスプリットを多投して活躍しました。そのスプリットは2021年のMLBの投手が投げる投球の中で、最も打ち難いボールとして賞賛されました。Baseball Savant から典型的な次の3球①143.7 km/h、1693rpm、②140.8 km/h、1432rpm、③138.6 km/h、1322rpmをピックアップすることにします。スプリット（フォークボール）と比較すると、回転数が高いという特徴があります。フォークアイによる縦方向と横方向の変化は、Baseball Savant によると①縦3.35cm、横3.96cm、②縦1.83cm、横11.89cm、③縦7.32cm、横-3.05cmとなっています。この3球をスプリットとして広く投げられているツーシーム回転で空力解析してみました。その結果は、①縦51.54cm、横-6.97、②縦47.28cm、横-5.01cm、③縦41.27cm、横5.56cmと、特に縦方向の変化がBaseball Savantの数値と全く違います。①の投球に対するボール周りの流れ（渦のようす）を動画で示します。速度勾テンソルの第二不変量の等値面を示していますが、高速なボールの飛翔により後流は激しい乱流となっています。低速回転のツーシームと違って、後流が絶えず下に向いています。ツーシーム回転しているけれど、回転数が高いために縫い目による正のマグヌス効果の方が負のマグヌス効果よりも大きくなっているため、強い揚力を受けていると言えます。

MLB中継の中で大谷投手の投げるスプリットの高速度カメラ映像（スローモーション）を確認すると、ツーシーム回転をしていません。ジャイロ回転をしてるように見えます。ジャイロ回転とは、下の動画のようにボールの回転軸が進行方向とほぼ一致していて、ライフルの弾丸やラグビーボールのパスなどで使われます。（下の動画）

球速143.7 km/h、1693rpmでジャイロ回転するボールの空力解析を行ってみました。計算条件は同じで、縫い目の回転だけが違います。計算結果の動画は、後流が上に向かったり下に向かったりしていることが分かります。

後流を背後（ピッチャー側）から見た動画を示します。後流がスワール（旋回）運動していることが分かります。つまり、ボールは1回転の中で上向きの力を受けたり、下向きの力を受けたり右向きの力を受けたり左向きの力を受けていて、平均（時間積分）すると殆ど空気から力を受けていません。

MLBの試合でのボール軌道の変化量（BS: Baseball Savant）と比較すると一目瞭然で、大谷翔平選手の投げているスプリットを、ツーシームのバックスピンではなく、ジャイロ回転している「ジャイロ・スプリット」と仮定すると、ほぼ一致します。

千賀滉大投手（ソフトバンク→ニューヨーク・メッツ）のフォークボールも、ソフトバンク時代から「お化けフォーク」と呼ばれ、鋭く落ちるボールを投げていました。そのスローモーション映像から「ジャイロ回転しているのでは」と噂されていました。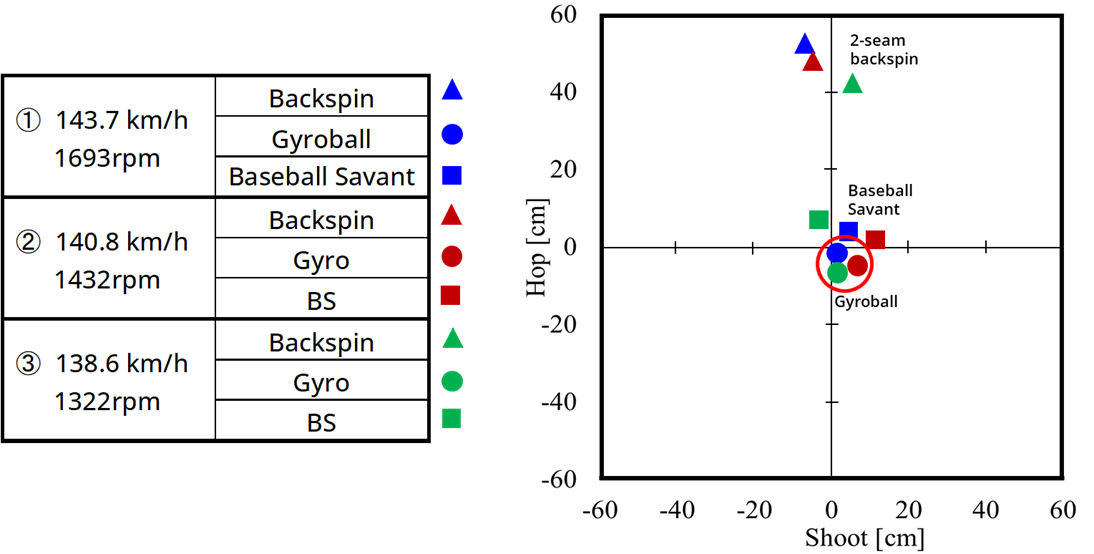

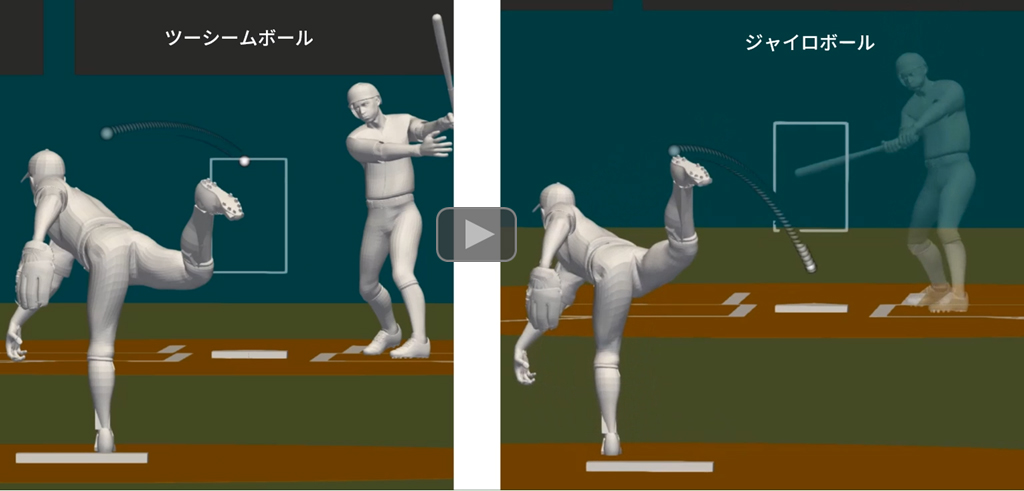
大谷選手のスプリットをツーシーム回転（左の動画）とジャイロ回転（右の動画）としたときのボール軌道を以下に示します。ジャイロ回転の場合、ホップ成分はなく、ボール軌道は重力だけの（ほぼ）放物線となります。ジャイロ回転についても、縫い目の向きでフォーシームジャイロとツーシームジャイロがあります。大谷選手のスプリットは、フォーシームジャイロのようです。

スイーパーが余り落ちずに横に大きく曲がる理由

2023年3月のWBC(World Baseball Classic)の日本と米国の決勝戦9回裏2アウト、大谷翔平投手とマイクトラウト選手の対決には誰もが釘付けになりました。そして、大谷投手がトラウト選手を三振に打ち取って日本が優勝し、日本中が歓喜の渦の中に巻き込まれました。空振りを取った最後の一休は（後にスイーパーという球種と認定される）横に大きく曲がるスライダーでした。

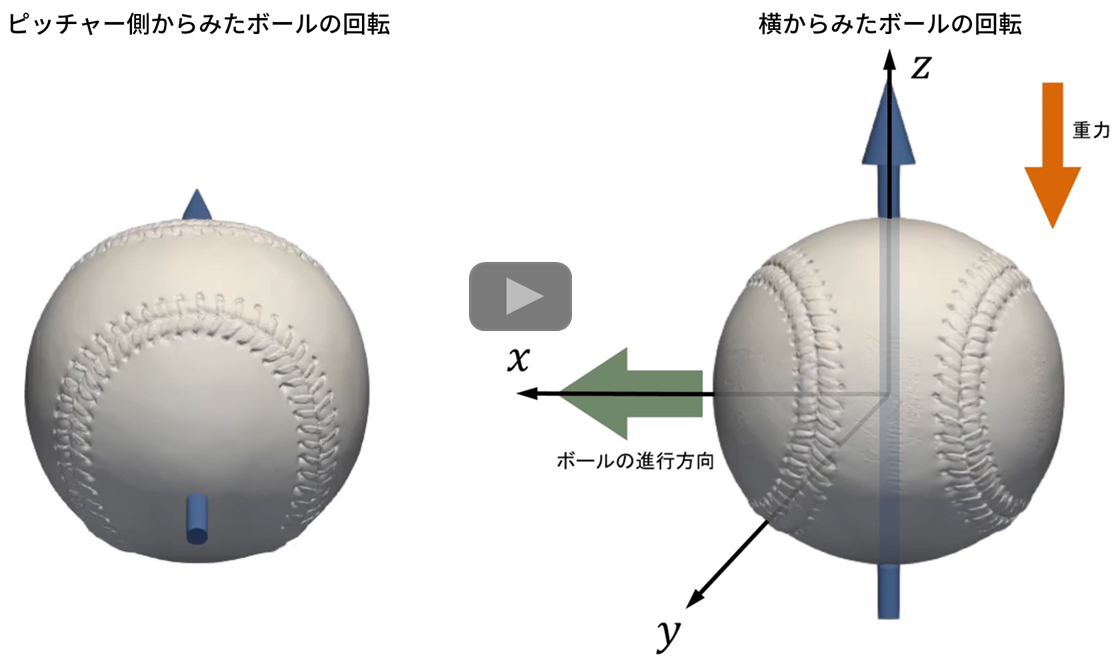
ボールが横に大きく曲がるので、ボールは横に高速回転していてマグヌス効果が働いていることは予想できます。しかしそれだと鉛直方向には重力でかなり落ちてしまいます。大谷投手がスイーパーを投げるときのスローモーション映像を詳しく見ると、スイーパーの回転は横回転だけではないことが分かります。下の左側の動画は、ツーシームの回転軸をバッター側に50度倒して回転させていて、スローモーション映像と酷似しています。右側は、回転軸を傾けたときの回転の様子を横から見た動画です。

回転軸がバッター側に傾く角度をαとすると、α=50度を保ったままボールの回転と移動を示したのが下の動画となります。

αが90度になると、完全なジャイロ回転となります。回転軸が傾くほど回転の効果がボーク軌道に反映しなくなるため、MLBなどではcos(α)を回転効率と呼んでいます。ストレートの場合は、回転数だけでなく回転効率が100%（α=0）に近いと、ボールのホップ成分が大きくなり、打たれ難いストレートになると考えられています。回転効率はフォークアイなどでも測定に難く、1球毎の回転効率はBaseball Savantでもデータに含まれません。
そこで、大谷投手のスイーパーの回転効率（回転軸の傾き）をパラメータとし、色々変えて空力シミュレーションを行ってみました。下の動画は回転効率を60%（回転軸の傾き 53度）としたときのスイーパーの空力シミュレーションの結果です。

高速で飛翔する野球ボールの周囲には境界層が発達します。縫い目はボールの面に対して突起となり、そこで境界層はボール表面に追従できず剥離が生じます。回転効率が約60%（傾き53度）のスイーパーは、ボールの上面と下面に縫い目が存在している時間が長いのが特徴です。上面の縫い目は少し上流側にあるため、縫い目で剥離した境界層がボールに再付着します。一方、下面は縫い目が少し下流にあるため、縫い目が境界層の剥離点となります。上面で再付着した境界層は、内部が乱流になっているため運動量交換が活発になっていて剥離し難い状態となり、上面の乱流境界層の剥離点は大きく下流に移動します。この上面と下面の剥離の違いが後流を下向きに変え、ボールには上向きの揚力が働くことが分かります。背面からシミュレーション結果を見ると、後流が斜め下向きに流れていることが分かります。つまり、その反作用の上向きの力と横向きの力を受けていることが確認できます。

スイーパーには、マグヌス効果ではない上向きの揚力が発生し、重力よる落下を抑制するため、余り落ちずに横に曲がる（横方向はマグヌス効果）ことが分かりました。

2022年後半から2023年にかけて大谷投手が多投したスイーパーの各投球の縦変化と横変化をプロットした図に本シミュレーションの結果を重ねてみました。回転効率は分からないため、3通りの回転数 2000rpm, 2300rpm, 2590rpmに対し、回転数を20%から80%まで振ってシミュレーションを行いました。また、大谷投手はスイーパーを投げる際に腕が少し下がり、サイドスロー気味になるため、回転軸をロール角方向に22.5度回転させて計算しています。その結果、MLB のデータと非常によく一致する結果が得られました。

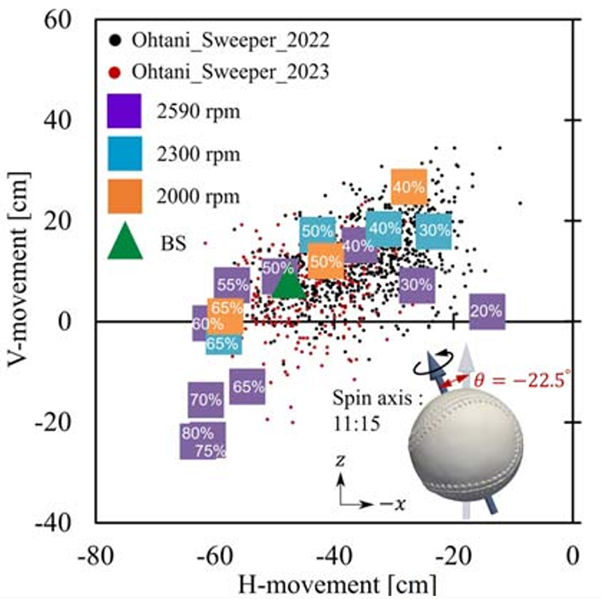
球速136.5km/hと回転数2590rpmのツーシーム・スライダー回転に対して、回転効率60%（回転軸の傾き53度）でシミュレーションした結果に基づき、スイーパーのボール軌道を再現しました。シミュレーション結果は、実際の映像のボール軌道と非常によく一致していることが分かりました。